Rope Body

Mesh Requirements#

The only acceptable mesh type for a Rope body is a cylinder. You can use a standard primitive cylinder to create a rope. The workflow in this case is as follows:

On the Menu bar, click Create -> Primitive -> Cylinder.
Specify desired rope parameters (length, radius) for a cylinder, e.g. the following:
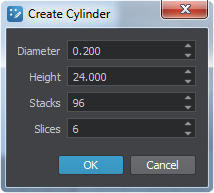
Click OK and place the cylinder somewhere in the world. It is created as a Static Mesh object. The object itself can be deleted, its mesh however is still available in the data/ folder.
Create a Dynamic Mesh object and use the cylinder mesh for it.
Assign the Rope body to the created dynamic mesh object.

Assigning a Rope Body#

To assign a Rope body to an object via UnigineEditor perform the following steps:

Open the World Hierarchy window.
Select a dynamic mesh object to assign a Rope body to.

Notice
Make sure that the object's mesh meets requirements!
Go to the Physics tab in the Parameters window and assign a physical body to the selected object by selecting Body -> Rope.
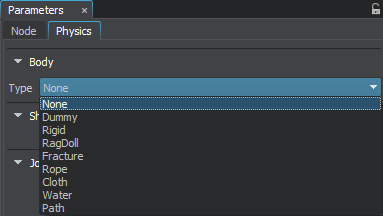
Set the body's name and change other parameters, if necessary.

Attaching a Rope#

Rope attached to a Mesh Skinned

Rope attached to animated character

Ropes can be attached to the following types of bodies:

To attach a rope to a body, use the Particles joint. In case of Rigid body (either static or dynamic) and Dummy body, pinned particles stay fixed in their position and follow transformations of attached objects pulling the rope with it.

Select Rigid body, RagDoll body or Dummy body.
Add Particles joint.
Specify Rope body.
Adjust the pinning area using the Threshold and Size parameters of the Particles joint.

NoticeTo ensure stable simulation it is important to set appropriate masses of the rope and the attached body. Unbalanced masses may cause twitching of rope joints.

Attachment to Skinned Mesh#

Convincing simulation of the rope on a Mesh Skinned character requires a different approach. To follow bones transformations, each vertex of the rope that is found in the Particles joint area is mapped to the nearest Mesh Skinned vertex (up to the distance specified by the Threshold parameter of the particles joint).

NoticeIt is not recommended to attach the rope directly to the Mesh Skinned character, because difference in topologies may result in visual artifacts. Instead, it is better to create an identical rope surface on the Mesh Skinned character, make it invisible and attach a physical rope to it.

For example, we need to create a rope that is glued to the hand of a Mesh Skinned character while the rest of the rope hangs and moves loosely. It is done in the following steps:

When creating a Mesh Skinned, add a rope segment surface identical to the clipped part that needs to be pinned. In our case, it's the rope part in a hand.
Add Mesh Skinned that has a RagDoll body assigned. Make sure that the rope segment surface is enabled.
Add a separate dynamic rope mesh and synchronize its position with Mesh Skinned character. Turn off physical simulation (CTRL + SPACE) and assign a Rope body.
Attach Rope body to RagDoll body. If the Threshold distance of the particles joint is set low enough, the physical rope will be automatically attached only to the rope segment surface (i.e. hand). After that, the rope segment surface is simply disabled and does not provide any load at all.

Parameters#

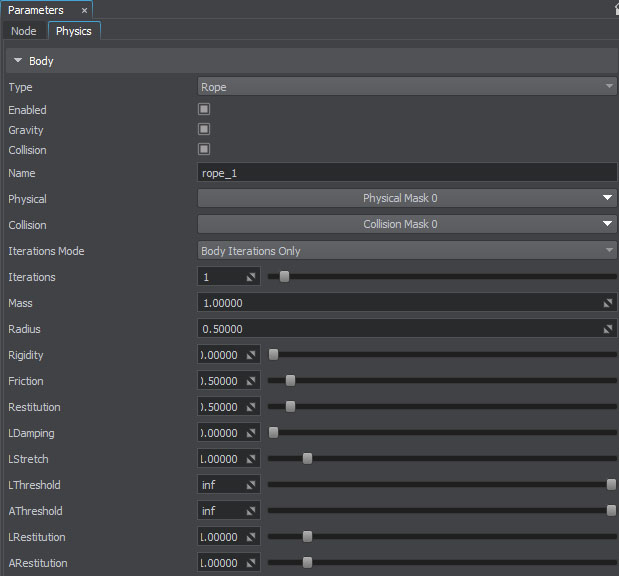
Gravity	Toggles the gravity for the body on and off.
Collision	Toggles collision detection for the rope body on and off.
Name	Name of the body. This name may become helpful for identification when creating joints, detecting contacts, handling callbacks, etc.
Iterations Mode	The mode that determines how the number of iterations for solving the constraints of the particles body is calculated. By selecting the suitable mode for each rope body you'll have flexibility in fine-tuning of performance and simulation quality. Body Iterations Only — the resulting number of iterations is equal to the value set for the body. *Global Iterations Body Iterations** — the resulting number of iterations is equal to the value set for the body multiplied by the global physics iterations number.
Iterations	The number of iterations controls the accuracy of the solution of rope inner joints. This number indicates how many times the joints are solved per physics frame. Joints are solved in a random order to provide more predictable stretching results. Low number of iterations results in faster simulation. However, in this case the rope is more prone to stretching and looks more elastic. The minimum value is 1. High number of iterations provides more accurate solution of constraints. In this case the rope looks stiffer. The maximum value is 16. Notice Increased number of iterations is considerably expensive and at some point ceases to bring a noticeable benefit, so it should be kept within a reasonable cost-effectiveness limit. Increasing the number of iterations may help to avoid twitching of a rope.
Mass	Mass of the body, in kilograms. Notice Do not use real masses, this can make physics simulation unstable. Adjust mass values when necessary to achieve realistic behavior (e.g. for a wheel mass of 25 kg it might be better to set 60 kg for a car body instead of 2000 kg). It is very important to ensure mass balance – avoid connection of too heavy bodies to very light ones, otherwise the joints may become unstable!
Radius	Radius of the particles forming the rope body and represented as sphere shapes. Rope particles use continuous collision detection, so higher values are preferable for more robust behavior. Collisions between the particles are not calculated and should not be considered when setting a radius. Be careful, however, as particles too big in diameter can provide incorrect interaction with environment (twitching or blowing up of the rope). Too low radius results in poor collision handling.
Rigidity	Additional constraint of the rope motion to control its stiffness and flexibility: Lower values make the rope elastic, flexible and easily deformable. Higher values make the rope stiffer and less prone to deformation.
Friction	Friction coefficient of the body, enables modeling of rough rubbing of surfaces. The higher the value, the less tendency the body has to slide.
Restitution	Coefficient of restitution determines the degree of relative kinetic energy retained after a collision. It defines how bouncy the object is when colliding with another object: Higher values result in more elastic collisions. Objects bounce off according to the impulse they get by contact. Lower values result in more inelastic collisions. Objects do not bounce at all.
LDamping	Linear damping reduces linear velocity of the body over time and slows it down up to a complete stop. Higher values make the body slow down faster. Global linear damping is added to the linear damping of the body to calculate resulting value.
LStretch	Linear stretch determines the scale for the length of linear joints (relative to the source mesh topology).
LThreshold	Linear threshold sets the distance limit for stretching the rope. When two particles move away from each other further than this limit, joints that connect them break and a the tear appears. Notice If set to infinity (inf), the rope is stretched without tearing. This value is set by default.
AThreshold	Angular threshold represents a maximum angle to fold the rope relative to its initial state. If set to infinity (inf), the rope is folded without tearing. This value is set by default. Notice It is recommended to keep the angular threshold lower or equal to 180 degrees.
LRestitution	Linear restitution determines how far the rope particles can be stretched apart from each other. It enforces rope joints to restore the distance that was between the vertices of the original mesh: Higher values make the particles spring back with greater force and the rope becomes harder to stretch. It gives the effect of a stiff non-stretch rope, e.g., a metal wire. Lower values make the rope more stretchable and elastic, e.g., a rubber cord. Notice 0 and near zero values are not allowed because they cause unstable simulation and blowing up of the rope.
ARestitution	Angular restitution determines the possible angle between rope triangles formed by particles. It constrains folding of the rope by enforcing joints to keep the angle that was between the triangles of the original mesh: At higher values, angles tend to be retained and the rope resists folding, it appears to be stiff. At lower values, the rope can be easily folded and bent in any direction, regardless of the original mesh topology. Setting up the maximum value (1.0) may provide unsteady behavior.

Mass-Spring Simulation Model#

The Rope body is modeled as set of point masses (particles) located in the mesh vertices. Each particle is represented with a sphere shape and linked to other particles by inner spring joints that are located along the mesh edges. Inner joints allow recreating the mesh topology as well as restricting stretching and folding.

Mass-Spring Simulation Model

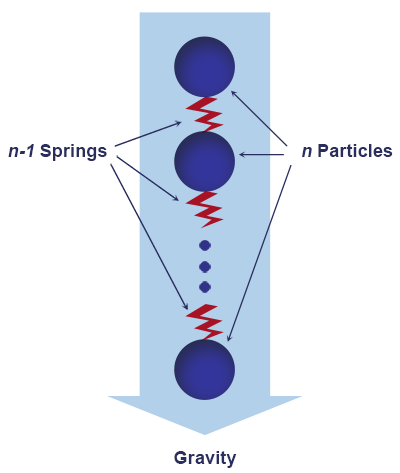
Each particle is characterized by a position, mass and velocity and has a constant spherical shape with a set radius. The total mass of the whole body is equally distributed among them. In accordance with Newton's second law particles can be acted upon by a force or an impulse applied by inner joints and external forces (collision, gravity, air resistance, wind, etc.).

Self-collision of the particles and collisions between different rope bodies are not calculated. However, the rope interacts with environment by colliding with other physical bodies if the Collision box is checked. Its behavior in case of contact is controlled by such parameters as friction and restitution. Selective physical interaction is available via corresponding bitmasks.

Thus, Rope body can be regarded as a constrained system of rigid particles and therefore shares with Rigid body such parameters as mass, friction, restitution, linear and angular damping.

Due to the fact that particles are represented by spheres, continuous collision detection is used for collisions with other objects. The rope never lies flat on the ground or tightly adheres to the surfaces. There is always a gap equal to particle radius.

Stretching and Folding#

A rope may be deformed by stretching and folding. These deformations are controlled with joint constraints of two types:

Linear restitution controls stretching.
Angular restitution controls folding.

With these types of constraints, it is possible to obtain the desired look and feel of the rope and simulate a variety of different deformable materials ranging from a stiff metal wire to an elastic rubber cord.

Notice

If the rope is too stretchy and rubbery, try one of the following:

Set linear restitution to 1.
Increase the number of joints solver iterations.
Use the mesh with fewer vertices.

Tearing#

When the rope is stretched or folded beyond its elastic limit, it tears and shreds into pieces. Tearing is caused by applying the force or collision with a physical body, and depends on the rope stiffness (controlled by linear and angular restitution parameters). The rope is torn only along the edges of rope triangles, splitting mesh vertices and duplicating particles.

Notice

If torn pieces of rope fall onto one plane, they cause Z-fighting.

Optimizing Simulation#

Updating each frame a huge number of objects located far away from the camera that are hardly distinguishable or observed as a mass is a waste of resources.

To improve performance and avoid the excessive load, simulation of the rope can be updated with a reduced framerate. When the player is out of the area specified by the Update Distance Limit, the rope stops to be updated and freezes statically.

The set of frame rates given below enables you to specify how often the rope simulation should be updated when the object is visible, when only its shadow is visible, or when it is not visible at all.

Parameters -> Physics tab -> Periodic Update section

FPS When Object Is Rendered To Viewport	Update rate value for the case when the object is rendered to viewport.
FPS When Only Object Shadows Are Rendered	Update rate value when the object itself is outside the viewing frustum, and only its shadow is rendered to viewport.
FPS When Object Is Not Rendered At All	Update rate value when both the object and its shadow are not rendered to the viewport.
Update Distance Limit	Distance from the camera up to which the object should be updated.

NoticeThese values are not fixed and can be adjusted by the Engine at any time to ensure best performance.

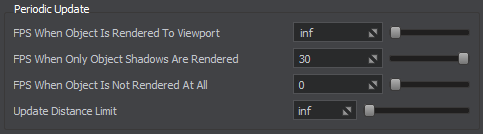
This feature is enabled with default settings ensuring optimum performance and can be adjusted per-object in the UnigineEditor or via API at run time.

WarningBe aware that using reduced update frame rate for an object should be carefully considered in your application's logic, as it may lead to various issues with rendering Mesh Skinned and Mesh Dynamic (flickering due to misalignment, e.g. in case of attaching a rope to a Mesh Skinned).

_{The information on this page is valid for UNIGINE 2.20 SDK.}

Last update: 2025-04-04

Help improve this article

Was this article helpful?

Report a problem related to this article

(or select a word/phrase and press Ctrl+Enter)